Sorting

Sorting is the process of arranging data in a particular format and order. Most common orders are elements of an iterable (List, Tuple, Array) numerical or lexicographical values. Sorting algorithm specifies the way to arrange data in some Alphabetical, Ascending or Descending order. For example: 1,5,2,3,4,6(Unsorted) and 1,2,3,4,5,6 (Sorted).

Alphabetical

Alphabetical order means every element is arranged in the same sequence as the letters of the alphabet. Example for characters: B,A,N,Q,P,M (Unsorted) and A,B,M,N,P,Q (Sorted). Example for strings: “Ajay”,“Aditya”,“Rohit” (Unsorted) and “Aditya”,“Ajay”,“Rohit” (Sorted).

Ascending

Ascending order means all elements of an iterable will be sorted in increasing manner (1, 2, 3, 4,...) Example: 10,54,100,25,75,90 Ascending >> 10,25,54,75,90,100.

Descending

Descending order means re-arranging all elements in decreasing order (... 10, 9, 8, …) Example data >> 1,2,5,4,3 Descending >> 5,4,3,2,1.

Types

There are many different available techniques for sorting:

• Bubble sort
• Selection sort
• Insertion sort
• Merge sort
• Quick sort

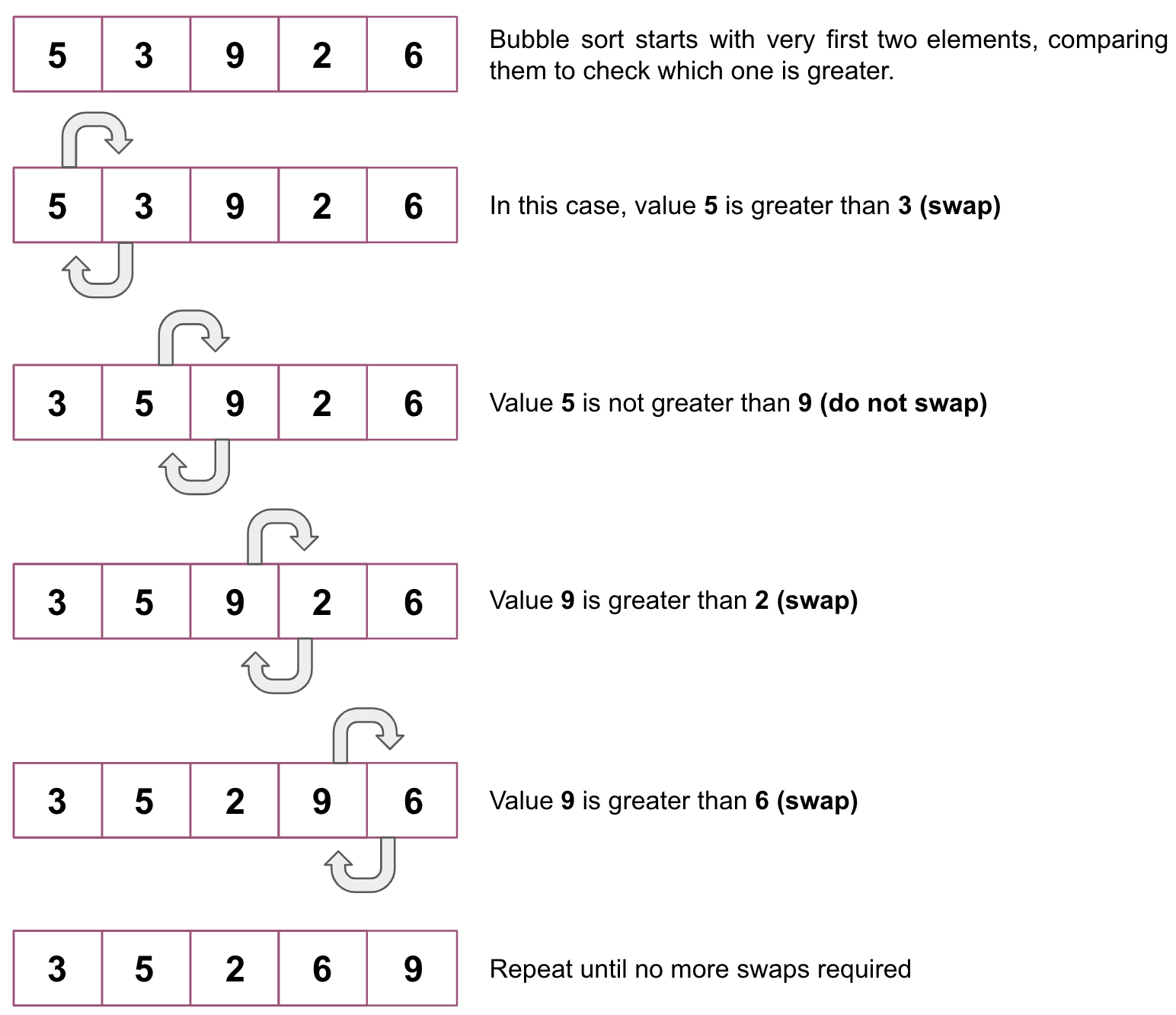
Bubble Sort

Bubble sort is a simple sorting algorithm, also known as sinking sort (comparison-based) in which each pair of adjacent elements is compared and the elements are swapped if they are in the wrong order. For example:

Code

def bubbleSort(list):
    for i in range(len(list)):
        for j in range(len(list) - i - 1):
            if list[j] > list[j + 1]:
                list[j + 1], list[j] = list[j], list[j + 1]
    return list

my_list = [5, 9, 1, 4, 2, 8, 0, 3, 7, 6]
print("Original list: \n", my_list)

print("List with bubble sort: \n", bubbleSort(my_list))

>>> Original list: 
>>> [5, 9, 1, 4, 2, 8, 0, 3, 7, 6]
>>> List with bubble sort: 
>>> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Note: this algorithm gets its name because elements tend to move up into the correct order like “bubbles” rising to the surface.

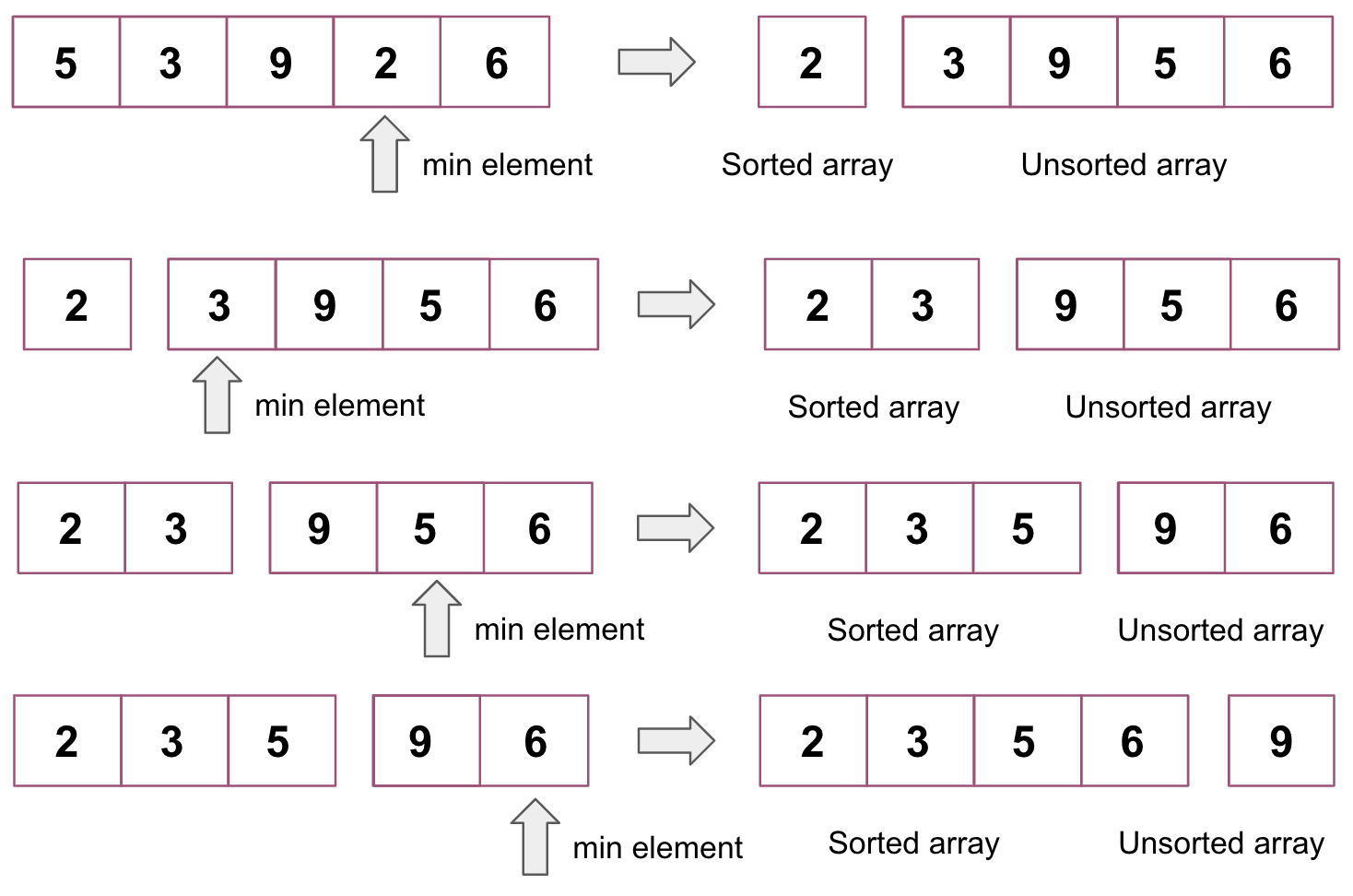
Selection Sort

The selection sort is an in-place comparison sorting algorithm in which the list is divided into two parts: the sorted part on the left end and the unsorted part on the right end. It's based on the idea of finding the minimum or maximum element in an unsorted list and then putting it in its correct position in a sorted list.
Basically, the smallest element is selected from the unsorted list and swapped with the leftmost element (this element becomes a part of the sorted list), then this process continues moving an unsorted list boundary by one element to the right.

Code

def selectionSort(list):
    for i in range(len(list) - 1):
        min = i
        for j in range(i, len(list)):
            if list[min] > list[j]:
                min = j
        list[i], list[min] = list[min], list[i]
    return list

my_list = [5, 9, 1, 4, 2, 8, 0, 3, 7, 6]
print("Original list: \n", my_list)
print("\nSorted list: \n ",selectionSort(my_list))

>>> Original list: 
>>> [5, 9, 1, 4, 2, 8, 0, 3, 7, 6]
>>> Sorted list: 
>>> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Insertion Sort

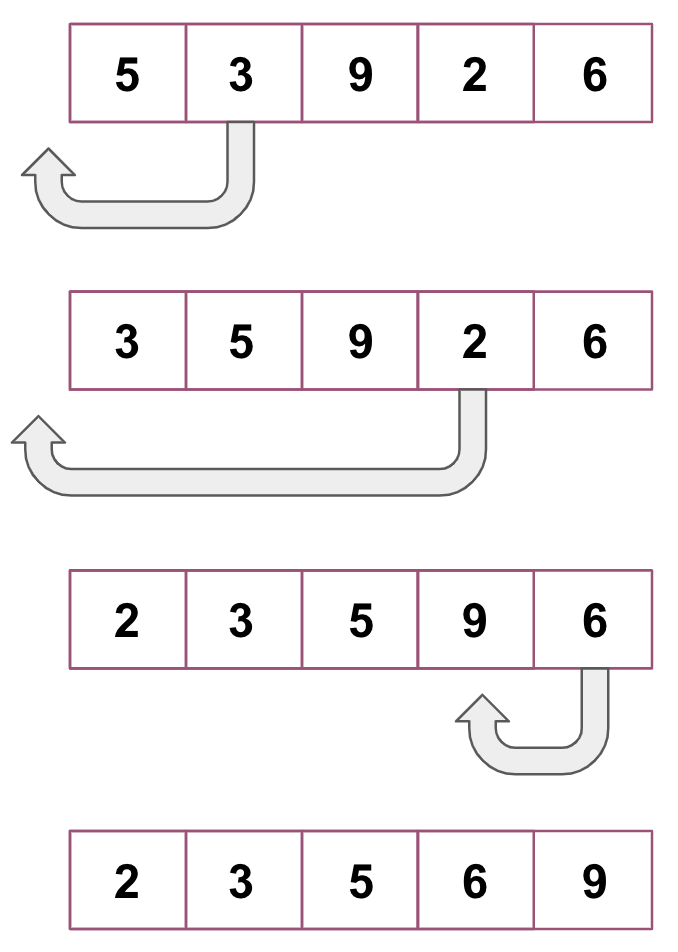
This is another in-place comparison sorting algorithm, where a sub-list is maintained and always sorted. Basically, the list is virtually split into a sorted and unsorted part. The list is searched sequentially and unsorted items are moved and inserted into the sorted part (same list). This algorithm is better than selection and bubble sort but is not suitable for large data sets as its average.

Code

def insertionSort(list):
    for i in range(1, len(list)):
        temp = list[i]
        j = i - 1
        while temp < list[j] and j >= 0:
            list[j + 1] = list[j]
            j -= 1
        list[j + 1] = temp
    return list

my_list = [5, 9, 1, 4, 2, 8, 0, 3, 7, 6]
print("Original list: \n", my_list)
print("List with insertion sort: \n", insertionSort(my_list))

>>> Original list: 
>>> [5, 9, 1, 4, 2, 8, 0, 3, 7, 6]
>>> List with insertion sort: 
>>> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Merge Sort

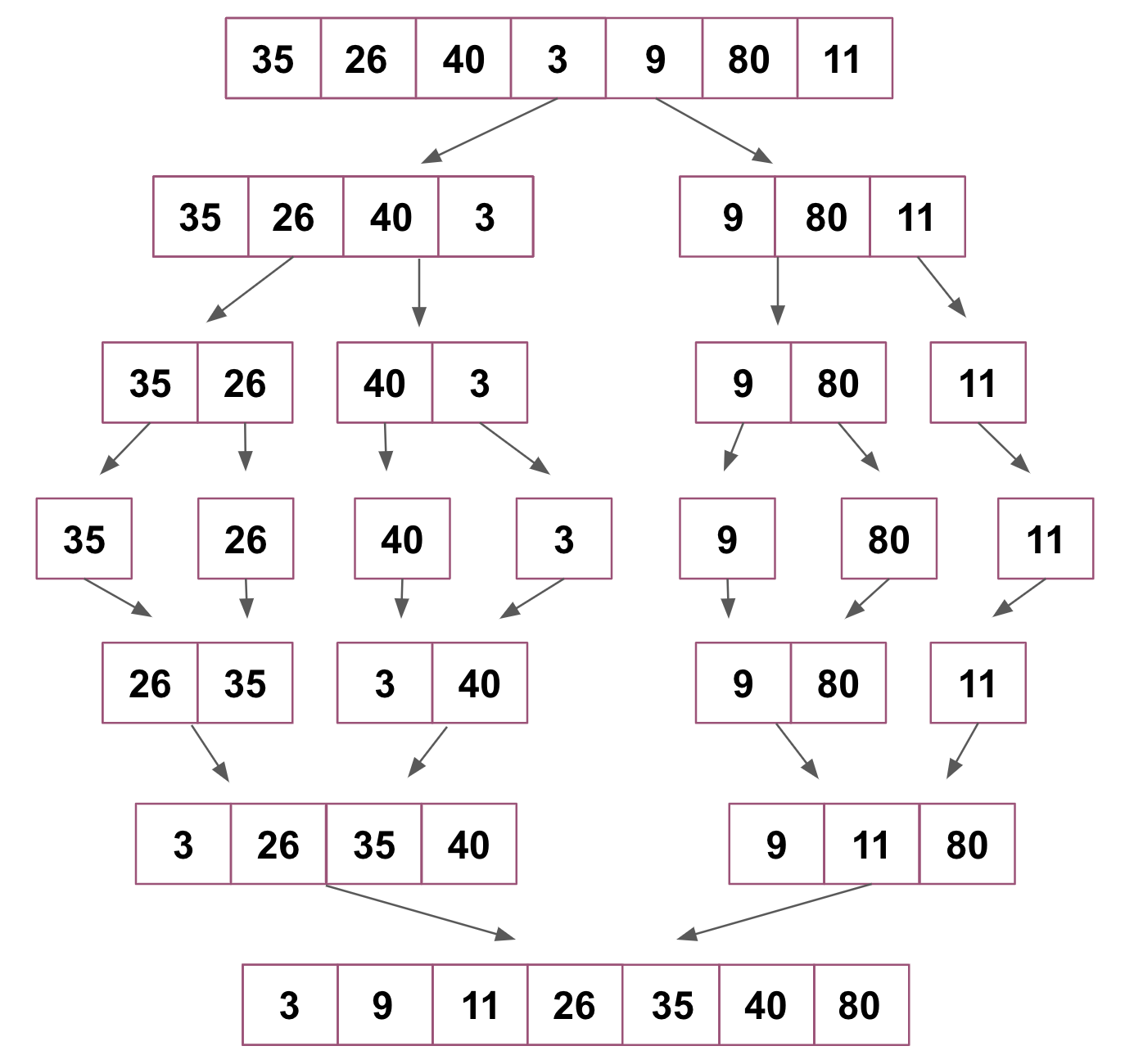
Merge sort is one of the most efficient sorting algorithms and works on the "Divide and Conquer" principle. Repeatedly, a list is divided into several sublists until each consists of a single element and then they are combined to obtain an ordered list as shown in the following example.

Code

def merge(list, left, mid, right):
    n1, n2 = mid - left + 1, right - mid

    L = [list[left + i] for i in range(n1)]
    R = [list[mid + 1 + j] for j in range(n2)]

    k = left
    while L and R:
        if L[0] <= R[0]:
            list[k] = L.pop(0)
        else:
            list[k] = R.pop(0)
        k += 1

    if L:
        list[k: k + len(L)] = L
        k += len(L)
    if R:
        list[k: k + len(R)] = R

    return list

def mergeSort(list, left, right):
    if left < right:
        mid = (left + (right - 1))//2
        mergeSort(list, left, mid)
        mergeSort(list, mid + 1, right)
        merge(list, left, mid, right)
    return list

my_list = [5, 9, 1, 4, 2, 8, 0, 3, 7, 6]
print("Original list: \n", my_list)
mergeList = mergeSort(my_list, 0, len(my_list) - 1)
print("\nSorted list: \n ", mergeList)

>>> Original list: 
>>> [5, 9, 1, 4, 2, 8, 0, 3, 7, 6]
>>> Sorted list: 
>>> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Quick Sort

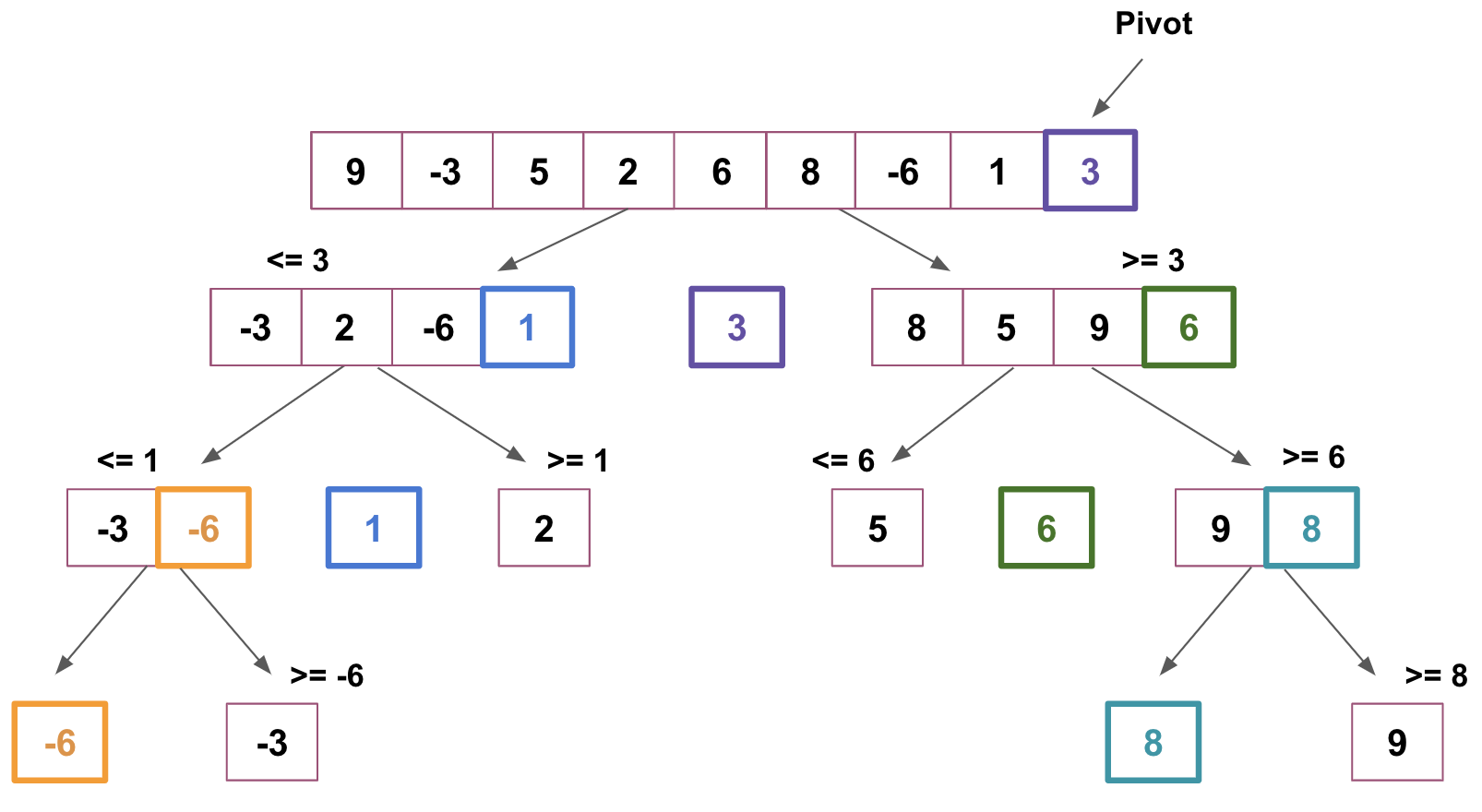
Quick sort is another algorithm based on partitioning a list of data into smaller lists. The list is partitioned into two lists:

1. The first one holds values smaller than the specified value (pivot) based on which the partition is made
2. The other list holds values greater than the pivot value

The algorithm calls itself recursively twice to sort the two resulting sublists.

Pivot

There are many ways to pick an element as a pivot.

1. Pick first element as a pivot
2. Pick last element as a pivot
3. Pick a random element as a pivot
4. Pick median as a pivot

Code

def partition(list, left, right):
    i = left - 1
    pivot = list[right]
    for j in range(left, right):
        if list[j] < pivot:
            i += 1
            list[i], list[j] = list[j], list[i]
    list[i + 1], list[right] = list[right], list[i + 1]
    return (i + 1)

def quickSort(list, left, right):
    if left < right:
        part = partition(list, left, right)
        quickSort(list, left, part - 1)
        quickSort(list, part + 1, right)
    return list

my_list = [5, 9, 1, 4, 2, 8, 0, 3, 7, 6]
print("Original list: \n", my_list)
quickList = quickSort(my_list, 0, len(my_list) - 1)
print("List with quick sort: \n", quickList)

>>> Original list: 
>>> [5, 9, 1, 4, 2, 8, 0, 3, 7, 6]
>>> List with quick sort: 
>>> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Github

Sorting Methods https://github.com/anto2318